クロスエントロピーとは

クロスエントロピーとは何か

クロスエントロピー（Cross-Entropy）は、分類問題で広く使用される損失関数の一つです。特にニューラルネットワークの学習において、モデルの予測精度を評価するために使われます。

クロスエントロピーの考え方は、モデルの予測確率が正解ラベルの確率分布にどれだけ近いかを測ることにあります。予測が正しいほど損失が小さく、誤った予測ほど損失が大きくなります。

---

クロスエントロピーの数式

クロスエントロピーは、ある確率分布 p(x)p(x) と、モデルが予測した確率分布 q(x)q(x) の間の誤差を測る指標で、次のように定義されます。

ここで、

• pip_i : 正解ラベルの確率分布（ワンホットエンコーディングの場合、正解クラスが1、その他は0）
• qiq_i : モデルの予測確率分布（Softmax関数などで算出）
• log⁡qi\log q_i : モデルの予測の対数値（予測値が1に近いほど損失が小さい）

この数式の意味は、正解ラベルに対応する予測確率の対数を取って、それを負の値にしたものです。正解クラスの確率が高いほど損失が小さく、低いほど損失が大きくなります。

---

クロスエントロピーの直感的な理解

クロスエントロピーの性質を理解するために、具体的な例を考えます。

ケース1: 良い予測

3クラス分類の問題を考えます。

• 正解ラベル（ワンホットエンコーディング）:
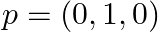
• モデルの予測確率:

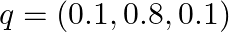
このとき、クロスエントロピー損失は

この場合、正解クラス（1の位置）の確率が高いので、損失は小さくなります。

ケース2: 悪い予測

次に、誤った予測の場合を考えます。

• モデルの予測確率:

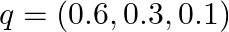
この場合のクロスエントロピー損失は

このように、正解クラスの確率が低くなると損失が大きくなります。

---

クロスエントロピーを使う理由

クロスエントロピーは、分類問題において以下のような利点があるためよく使われます。

1. 確率分布を扱うのに適している

モデルの出力が確率分布として解釈できるため、分類問題の評価に最適です。

2. 勾配降下法に適している

誤差が大きくなると勾配が大きくなり、学習がスムーズに進みます。

3. Softmax関数との相性が良い

出力層にSoftmax関数を使うと、クロスエントロピー損失が尤度最大化の最適化と一致し、理論的に合理的な損失関数となります。

---

実際のコード（PyTorch）

以下は、PyTorchでクロスエントロピー損失を計算する例です。

import torch
import torch.nn as nn

# モデルの出力（Softmax の前のロジット）
logits = torch.tensor([[2.0, 1.0, 0.1]])  # 1サンプル、3クラスのロジット

# 正解ラベル（クラス 0）
labels = torch.tensor([0])  # ラベルは 0（ワンホットベクトルにしない）

# クロスエントロピー損失関数
criterion = nn.CrossEntropyLoss()
loss = criterion(logits, labels)

print(loss.item())  # クロスエントロピー損失を出力

PyTorchの nn.CrossEntropyLoss() は内部で Softmax を適用してから損失を計算してくれるので、ロジット（Softmax 前の値）をそのまま入力できます。

---

まとめ

• クロスエントロピー損失は分類問題の学習に適した損失関数。
• 正解の確率を高めると損失が小さくなる。
• Softmax関数と組み合わせることで確率分布を最適化。
• 深層学習で広く使われる。

クロスエントロピーの概念を理解し、適切に活用することで、より効果的な機械学習モデルの構築が可能になります。