目次
データ前処理:特徴量の分布・相関・異常値の確認
特徴量のヒストグラム
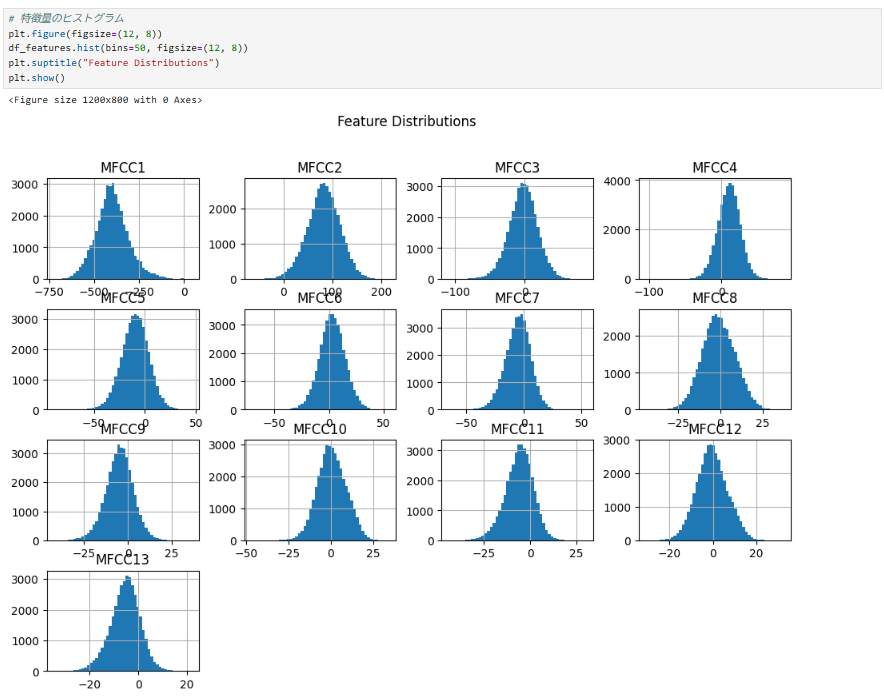
🔍 何を示しているのか?
- 各MFCC特徴量(MFCC1~MFCC13)の値の分布を確認するためのヒストグラム。
- X軸は各特徴量の値、Y軸はその値が登場する頻度(カウント)。
💡 ここから分かること
- 正規分布に近い形をしている特徴が多い。
- MFCC1 など、一部の特徴量が極端に分布の幅が大きい(スケールが異なる)。
- 対策:標準化(正規化)を行い、スケールを揃える必要がある。
- 左右非対称な分布がある(MFCC1 など)。
- 対策:対数変換や Box-Cox 変換を検討。
特徴量の箱ひげ図(Box Plot)
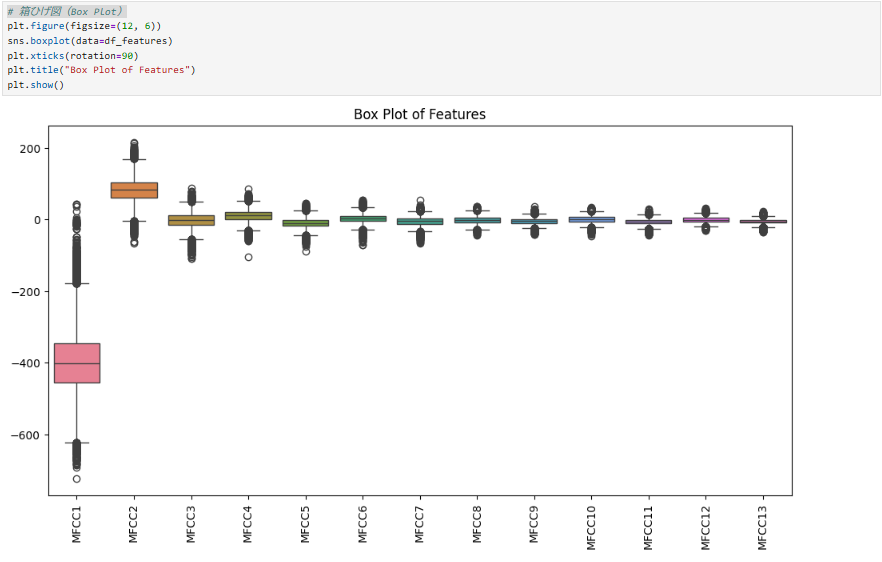
🔍 何を示しているのか?
- 各特徴量の値の範囲、中央値、外れ値を示す。
- 外れ値(異常値)があるかどうかを確認 するためのプロット。
💡 ここから分かること
- MFCC1 の範囲が極端に広い → 先ほどのヒストグラムと一致する結果。
- 一部の特徴量に外れ値(異常値)がある → 正しく処理しないとモデルの学習に悪影響を与える。
- 対策:外れ値をクリッピング(一定範囲に収める)や、異常値を削除する。
- ほとんどの特徴量は、中央値付近にデータが集中している → 分布が安定している特徴もある。
特徴量間の相関(ヒートマップ)
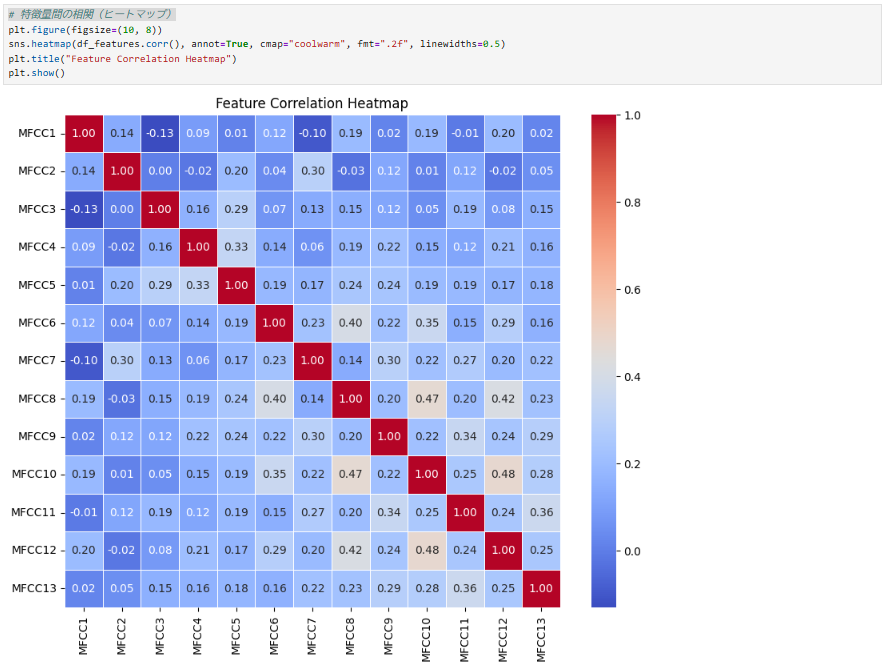
🔍 何を示しているのか?
- 各特徴量同士の相関関係を示す。
- 1.0 に近いほど強い相関(赤色)、0 に近いほど相関なし(青色)。
💡 ここから分かること
- MFCC4 と MFCC5, MFCC10 と MFCC11 など、強い相関がある特徴がある。
- 対策:冗長な特徴量を削除することで、モデルの計算コストを削減できる。
- 逆に、MFCC1 や MFCC8 など、ほぼ相関がない特徴もある。
- 個々の特徴が独立している場合は、そのまま使う方が良い。
データにスケールの違いや異常値があるため、前処理が必要。強く相関する特徴量は削除を検討する(不要な次元削減)。データの分布が異常な特徴(MFCC1 など)は、標準化を適用する。
結論
- データにスケールの違いや異常値があるため、前処理が必要。
- 強く相関する特徴量は削除を検討する(不要な次元削減)。
- データの分布が異常な特徴(MFCC1 など)は、標準化を適用する。
次は、以下の前処理を行う:
- 不要な特徴量の削除
- 正規化(Min-Max Scaling、標準化など)
- ノイズ除去、異常値の処理
- 必要に応じてデータ拡張(Data Augmentation)