ニューラルネットワーク(１)

ニューラルネットワークとは

深層学習は、ニューラルネットワーク（neural network）と呼ばれるアーキテクチャで実現される。これまでに学習した単回帰、重回帰、線形分類モデルは、一つの層から構成されるニューラルネットワーク、すなわち単層ニューラルネットワーク（single-layer neural network）と見なすことができる。また、ニューラルネットワークの学習には確率的勾配降下法（SGD）、およびその亜種（RMSPropやAdamなど）が用いられます。


参考元：ニューラルネットワーク (1) — 機械学習帳
参考元：ニューラルネットワークとは？基礎や仕組み、種類を解説



ニューラルネットワークの基本構造

ニューラルネットワークは、層（layer） によって構成され、一般的に以下の3つの層を持ちます。

入力層（Input Layer）

・データ（数値、画像のピクセル値、音声波形など）がこの層に入力される。
・各ノード（ニューロン）は、特徴量に対応している。

隠れ層（Hidden Layer）

・入力データの特徴を抽出する層で、1層以上存在する。
・各ニューロンは、前層のニューロンの出力を受け取り、重み付きの計算を行い、活性化関数を通じて次層に送る。

出力層（Output Layer）

・最終的な予測結果を出力する。
・例えば、2クラス分類なら2つのノード（Softmax関数）、回帰なら1つのノード（線形関数）を持つ。
　※ 出力層のタスク種類と２クラス分類

異なる役割を持つ複数の層で構成される

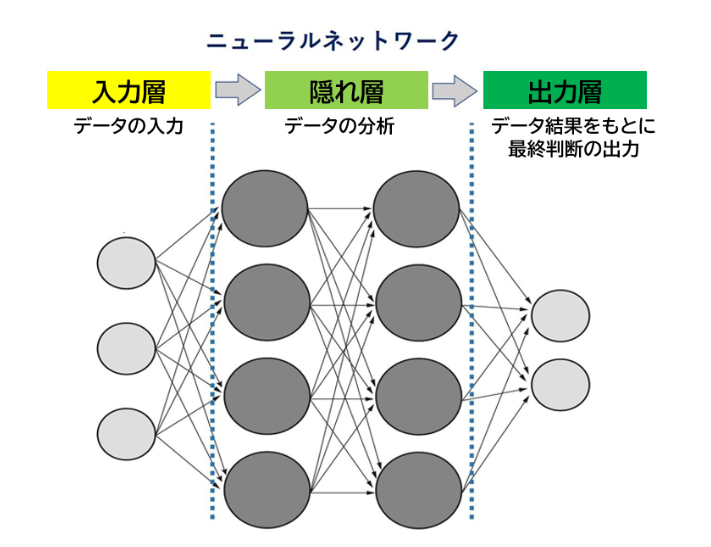
ニューラルネットワークは、分析の元となるデータが入力される「入力層」、入力されたデータの分析を行う「隠れ層」、データを出力する「出力層」の3層で構成され、脳神経系のように細かく結びついています。

隠れ層を何層も持つことで、より複雑かつ高度な処理が可能になります。

隠れ層で情報の重みが設定できるため、隠れ層の数を増やすことで、複雑な判断や細かな処理が可能になります。ディープラーニングの「ディープ」は、ニューラルネットワークの隠れ層について言及しており、報を処理する隠れ層の階層が多い、つまり深いことを意味しています。

重み という調整手法で結果を出力する

ニューロンとそのネットワークの考え方　

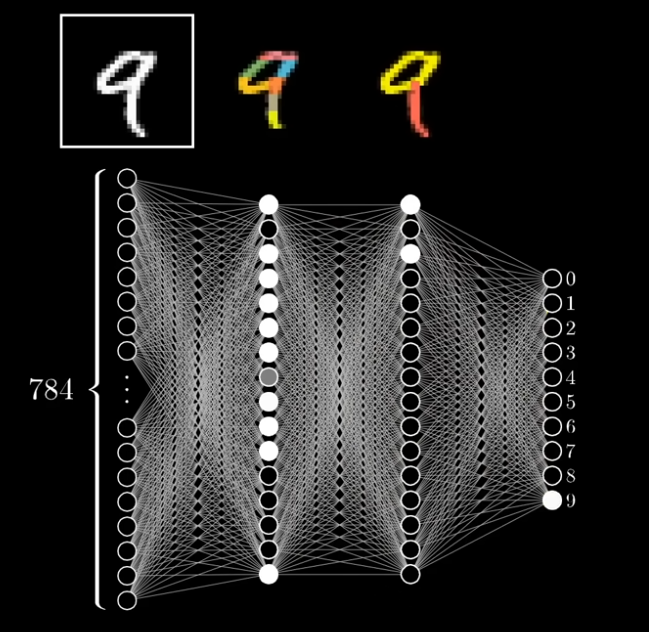
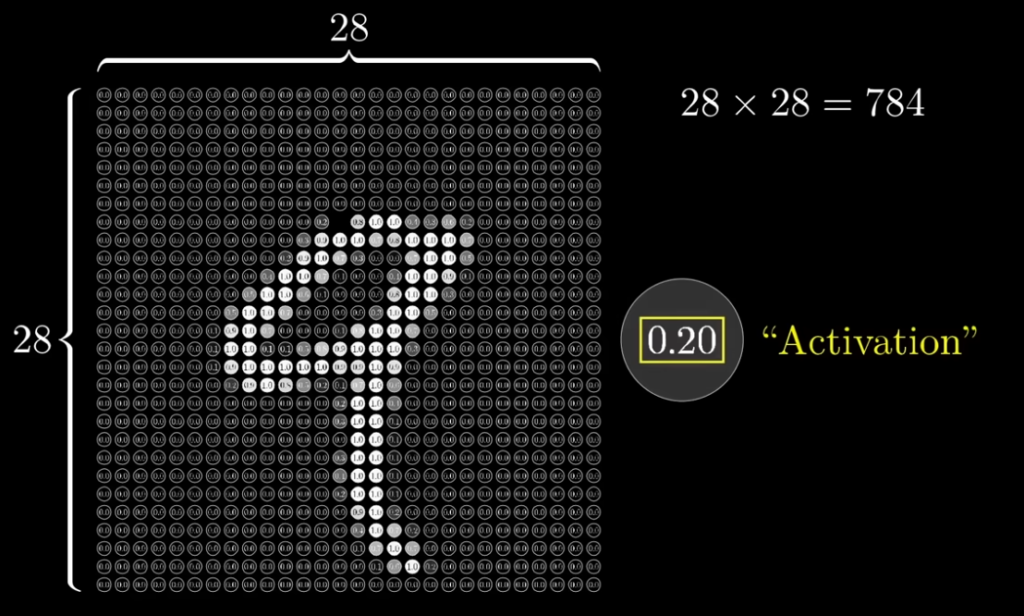
例として、以下図のように、28×28ピクセルのマス目に分割した７８４の盤面に数値を表現する。７８４の盤面に数値の状態から、結果が可視化して見た時には、０～９ のどの数値なのかという判断をしたいとする。目視ならば簡単ではあるが、プログラムを実装するとなるとそうもいかない。この ７８４の１つ１つをニューロンと考える。白く光っているニューロンは１.０に近い値で、暗いものは０.０に近い値であることが分かる。

ニューロンのアクティベーション（活性化）

１つのニューロンについて、ニューロンがどれくらい活性化しているかを表す数値とする。ここでは明度が高い方が１.０に近く、０.０になれば明度が落ちるような表現になっている。このアクティベーション値については、活性化関数を通して得られる。

中間層にある隠れ層でデータを分析する。データを分析したのち、出力層に至る。この際の隠れ層の処理は、学習データを元に訓練を行う部分になるのだろう。どのような処理かは分からないが、9 が正解に最も近ければ入力層から出力層へは、「９」という出力結果に至るはずだ。

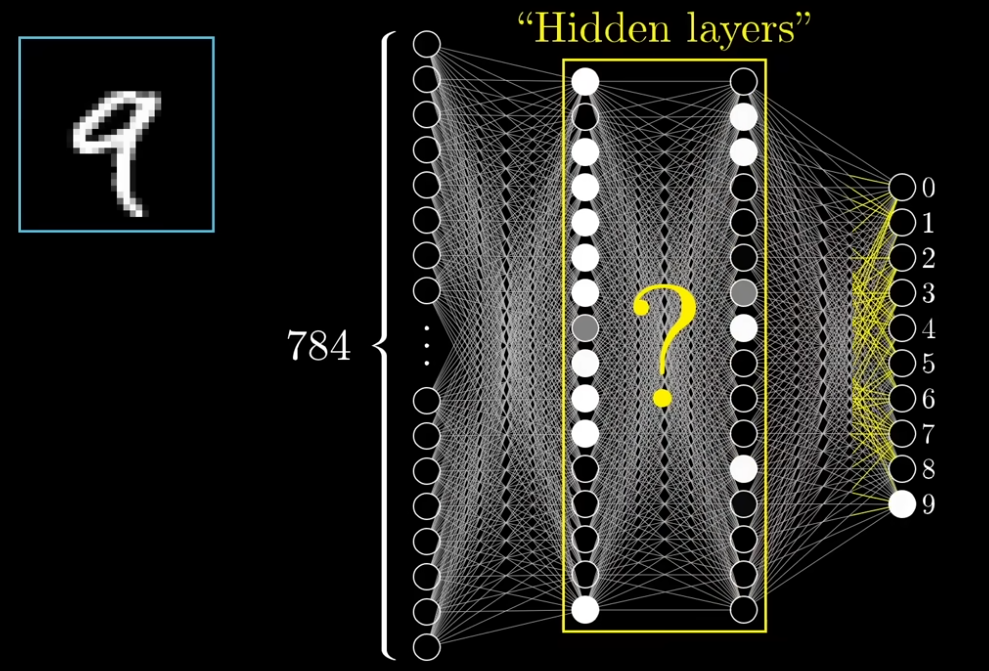
例えば、２層目で分析、細かい形状を抽出、３層目で分析した、「円形状・縦線の形状」のような形のニューロンが点灯、出力層では９が点灯する、ような流れにしたいところということのようだ。

ニューラルネットワークのアクティベーションの流れ

ニューラルネットワークにおけるアクティベーション（Activation） とは、各ニューロン（ノード）がどれだけ活性化しているかを示す数値です。この仕組みを理解することで、機械学習モデルがどのようにデータを処理しているのかを把握しやすくなります。

1. 入力（ピクセル値）

  • MNISTデータセット では、手書きの「9」のような画像が ２８×２８ピクセル（７８４個の入力） に分解されます。
  • 各ピクセルは、白い部分が 明るく（１.０）、黒い部分が 暗い（０.０） というように、０〜１の値 を持ちます。

2. 重み（Weight）とバイアス（Bias）を適用

ニューラルネットワークの各ノード（ニューロン）は、前の層の入力（ピクセル値）に 重み WW を掛け、バイアス b を足します。
この計算は以下のように表されます：

z = W \cdot x + b

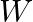  • W : 各入力に対応する重み（学習によって調整される値）
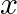  • x : ピクセルの入力値（0〜1）
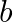  • b : バイアス（モデルの調整用パラメータ）

この計算結果 zz は、次の活性化関数に送られます。

3. 活性化関数（Activation Function）を適用

活性化関数を適用することで、非線形変換を行い、より複雑な関係を学習 できるようになります。
代表的な活性化関数には以下があります：

  • ReLU（Rectified Linear Unit）
    • f(z) = \max(0, z)
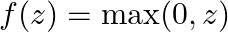
    • 負の値を0にし、正の値はそのまま保持。
    • ディープラーニングで最もよく使われる。
  • シグモイド（Sigmoid）
    • a = \sigma(z) = \frac{1}{1 + e^{-z}}
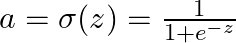
    • 0〜1の範囲に変換し、確率的な解釈が可能。
    • ニューラルネットワークの出力層（2値分類など）で使われる。
  • ソフトマックス（Softmax）
    • \sigma(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}}
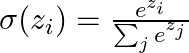
    • 多クラス分類で使用される活性化関数。
    • 出力が 確率分布 になる。

4. アクティベーション値の決定

活性化関数を適用することで、最終的なアクティベーション値（Neuronの出力） が決定します。
この値が次の層へ伝播され、最終的な予測結果を導きます。

第１層から第２層にニューロンを伝播する

下の図は第１層（入力層）から第２層（隠れ層）へニューロンが伝播する様子 を示している。
これを第２層のｎ個の隠れ層へ、引き渡す必要がある。

７８４個の情報とバイアスを、活性化関数を使い、一つの値を出したところである。
第２層が別画像を参考に、１６個のニューロンあると仮定すれば、それぞれのアクティベーション値が求められるため、この計算が１６回、必要になる。結構煩雑で、ぱっと見た感じ、大変そうである。

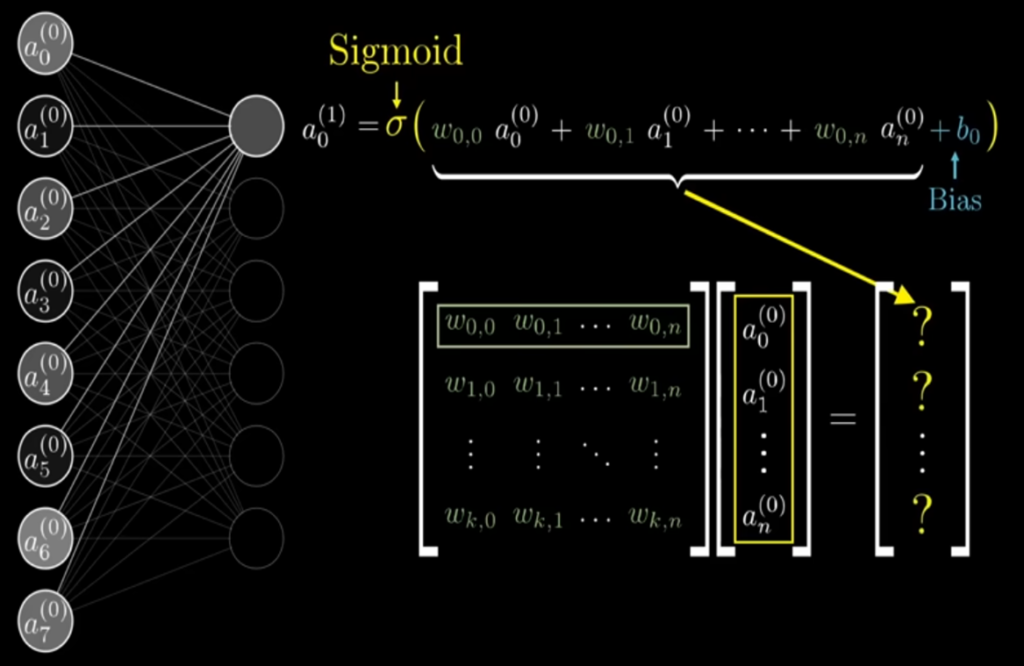
なので、重みは行列として計算され、全てのアクティベーション値はベクトルとして表される。
さらにバイアスもベクトルの形で保持されることで、1つの層から次の層へのアクティベーションの伝播を、行列演算としてコンパクトに表現できる。

a^{(1)} = \sigma(W a^{(0)} + b)

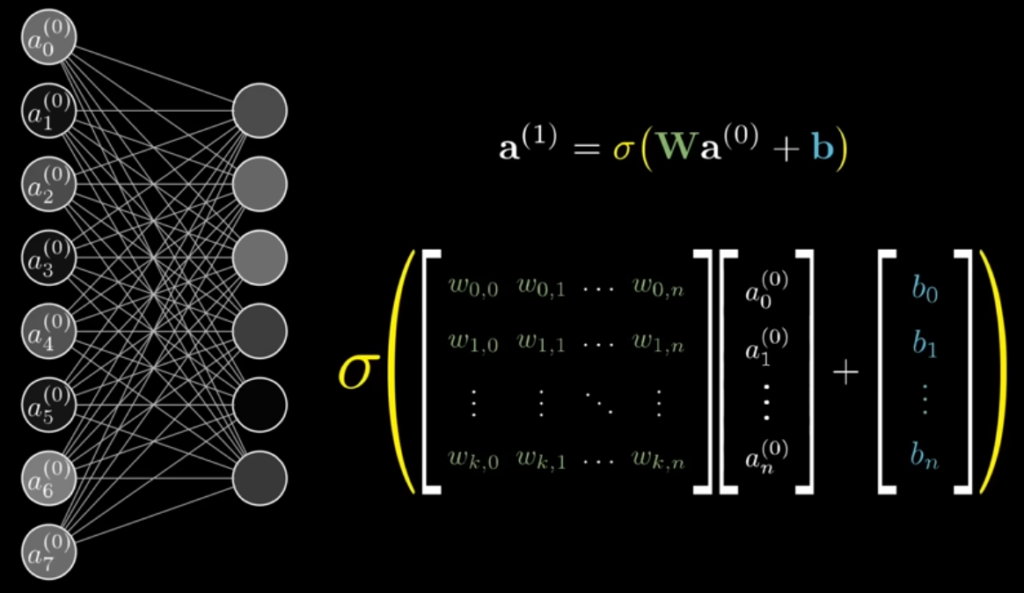
この式では、784個の入力値（ベクトル）と、重み行列 W をかけ算し、バイアスベクトル b を加えた後、活性化関数 σ\sigmaσ を適用することで、第２層の各ニューロンのアクティベーション値が求められる。

まとめ

✅ アクティベーションは、ニューロンがどれだけ活性化しているかを示す数値。
✅ ニューラルネットワークでは、入力に対して重み付きの線形変換を行い、その後活性化関数を適用する。
✅ 活性化関数を使うことで、ネットワークは非線形性を持ち、複雑なパターンを学習できるようになる。