目次
ベクトルと行列の基本
この記事では、「スカラー」「ベクトル」「行列」について基礎的な概念を解説します。これらは数学やプログラミング、データ分析など、多くの分野で使用される重要な概念です。
スカラー(Scalar)
スカラーとは、1つの値(数値)で表されるものです。
スカラーは大きさ(値)のみを持ち、方向の概念はありません。
- 例
これらは全てスカラーの例であり、それぞれ単独の数値を表します。
![]()
- 特徴:
- スカラーは、日常的な数値のように単純なもの。
- 実世界の例:温度(
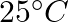 )、質量(
)、質量(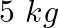 )、時間(
)、時間(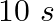 )など。
)など。
ベクトル(Vector)
ベクトルは、複数の要素を持つ値の集まり(1次元配列)を表します。
ベクトルは「大きさ」と「方向」を持ち、数学では通常、縦ベクトル(列ベクトル)または横ベクトル(行ベクトル)として表現されます。
縦ベクトルの例:
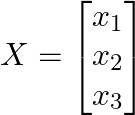
一般的なベクトルの表記:
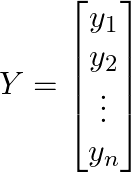
特徴:
- ベクトルの要素数(次元)は、データや問題の内容に応じて異なります。
- 実世界の例:
- 座標(例:2次元空間では
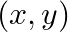 、3次元空間では
、3次元空間では 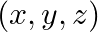 )。
)。 - 物理の速度ベクトル(例:速度の大きさと方向を同時に表す)。
- 座標(例:2次元空間では
行列(Matrix)
行列は、スカラーやベクトルを拡張したもので、行と列を持つ2次元の配列です。
行列は、複数のベクトルをまとめて表現する場合や、複雑なデータや計算を扱う際に使用されます。
行列の例:
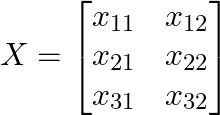
特徴:
- 行列は「行」と「列」の組み合わせから成り、行列のサイズ(次元)は「行数 × 列数」で表されます。
- 例:上記の行列
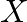 は
は  のサイズを持つ行列です。
のサイズを持つ行列です。
- 例:上記の行列
- 実世界の例:
- データ表(行がサンプル、列が特徴量)。
- コンピュータビジョンでの画像データ(ピクセル値の行列)。
図の役割と意義
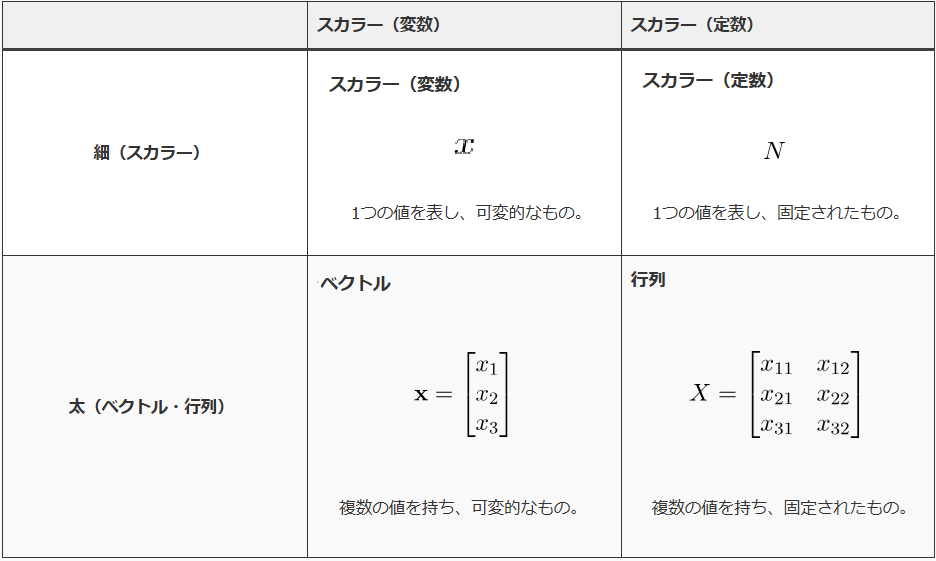
以下の図では、「スカラー」「ベクトル」「行列」を「変数か定数か」「単純か複雑か」の観点で分類しています。
- 横軸:値の種類
- 小(変数)⇔大(定数)
- 「小」は可変的な値(例:変数)を意味します。
- 「大」は固定された値(例:定数)を意味します。
- 小(変数)⇔大(定数)
- 縦軸:表現の形
- 細(スカラー)⇔太(ベクトル・行列)
- 「細」は単純な形(スカラー:1つの値)を意味します。
- 「太」は複雑な形(ベクトル・行列)を意味します。
- 細(スカラー)⇔太(ベクトル・行列)
スカラー、ベクトル、行列の分類表
スカラー、ベクトル、行列の関係性について
これらは次のような階層的な関係にあります
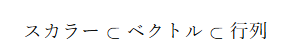
これが「スカラー」「ベクトル」「行列」の基本的な考え方です。
記号「⊂」の意味と式の解釈
この数式
「スカラー ⊂ ベクトル ⊂ 行列」
には、集合の包含関係を表す記号 「⊂」(部分集合) が使われています。
「⊂」の意味
数学では、記号「⊂」は 「部分集合(proper subset)」 を意味します。
A ⊂ B なら、「A は B の一部であるが、A と B は完全には一致しない」という意味になります。
この式の意味
この数式![]()
は、スカラー、ベクトル、行列の関係を階層的に表現 しています。
- スカラーはベクトルの一部である(スカラー ⊂ ベクトル)
- スカラー(単一の数値)は、次元が 1 のベクトルとみなすことができます。
- 例えば、スカラー x は、1次元のベクトル
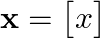 として表現できます。
として表現できます。
- ベクトルは行列の一部である(ベクトル ⊂ 行列)
- ベクトル(1列または1行の数値の集合)は、行列の特殊な場合とみなせます。
- 例えば、ベクトル
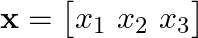 は、1列の行列(n×1 の行列) として扱えます。
は、1列の行列(n×1 の行列) として扱えます。
まとめ
この式が示しているのは、
- スカラーはベクトルの特別な場合である(1要素のベクトルとも考えられる)。
- ベクトルは行列の特別な場合である(1行または1列の行列とも考えられる)。
つまり、
スカラー ⊂ ベクトル ⊂ 行列 という関係は、スカラーが最も単純なデータ形式であり、そこからベクトル、行列とデータ構造が拡張されていくことを示しています。
補足
もし厳密な数学記号を使う場合、「⊂」ではなく「⊆」(部分集合の包含記号)を使うこともあります。
- 「⊂」 は「真部分集合(proper subset)」で、「A ⊂ B」なら A ≠ B(AはBの完全な一部)
- 「⊆」 は「部分集合(subset)」で、「A ⊆ B」なら A = B も許される
ここでは、「スカラーはベクトルの特別な場合であり、完全に含まれる」と解釈しているため「⊂」を使用していますが、「⊆」でも大きな意味の違いはありません。
次はこれらを使用して具体例を記事にします。
ベクトルと行列の基本(具体例)