勾配降下法とは？機械学習における最適化の基礎

---

1. 勾配降下法とは？

勾配降下法（Gradient Descent）とは、機械学習やディープラーニングのモデルが最適なパラメータ（重みやバイアス）を見つけるための最適化アルゴリズム です。

モデルは、誤差（損失関数の値）を最小化するようにパラメータを調整する 必要があります。勾配降下法は、この誤差を減らしながら、より良いモデルを作るための手法です。

2. 勾配降下法の概念

勾配降下法の基本的な考え方は、「高い場所から低い場所へ向かって降りる」というシンプルなものです。
数学的には、関数の傾きを計算し、その傾きに沿って誤差を減らしていきます。

勾配降下法のイメージ

1. 初期の重み（適当な値）からスタート
2. 損失関数の傾きを計算
3. 誤差が小さくなる方向にパラメータを更新
4. 誤差が最小になるポイント（最適解）を目指す

3. 数学的な仕組み

勾配降下法では、「損失関数」の微分（勾配）を計算し、パラメータを少しずつ更新します。

パラメータの更新式

各記号の意味

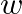• ：重み（パラメータ）
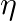• （イータ）：学習率（Learning Rate）
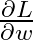• ：損失関数 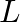の勾配（微分）

ポイント

• 勾配が正の場合 → 重みを減らす（右方向へ移動）
• 勾配が負の場合 → 重みを増やす（左方向へ移動）
• これを繰り返し、最適なパラメータを求める

4. 学習率（Learning Rate）の重要性

学習率（）は、勾配降下法のステップサイズを決める重要なパラメータです。

学習率	特徴	問題点
大きすぎる	更新量が大きく、素早く学習が進む	最適解を飛び越えて発散する可能性がある
小さすぎる	誤差が徐々に減る	収束が遅く、時間がかかる

適切な学習率を設定しないと、モデルが最適なパラメータを見つけられなかったり、学習に時間がかかりすぎたりするため、調整が必要です。

5. 勾配降下法の種類

勾配降下法には、データの使い方によっていくつかのバリエーションがあります。

種類	特徴	メリット	デメリット
バッチ勾配降下法 （Batch Gradient Descent）	全データを使って更新	安定した学習	計算コストが高い
確率的勾配降下法 （Stochastic Gradient Descent, SGD）	1つのデータごとに更新	計算が速い	学習が不安定で収束しにくい
ミニバッチ勾配降下法 （Mini-Batch Gradient Descent）	少数のデータをまとめて更新	バッチとSGDのバランス型	適切なバッチサイズの選択が必要

それぞれの使い分け

• データ量が少ない場合 → バッチ勾配降下法
• データ量が多く、計算コストを抑えたい場合 → ミニバッチ勾配降下法
• リアルタイム処理が必要な場合 → 確率的勾配降下法（SGD）

6. まとめ

✅ 勾配降下法は、誤差（損失）を減らすためにパラメータを更新する最適化手法
✅ 関数の勾配を計算し、誤差が小さくなる方向へ進む
✅ 学習率の調整が重要で、適切に設定しないと学習がうまく進まない
✅ 「バッチ」「SGD」「ミニバッチ」の3種類があり、用途によって使い分ける

ディープラーニングでは、勾配降下法をベースにした高度な最適化手法（Adam, RMSprop など）も使用されます。これらを理解することで、より効率的なモデルの学習が可能になります。