勾配降下法をベースにした高度な最適化手法

勾配降下法をベースにした高度な最適化手法

勾配降下法は、機械学習やディープラーニングにおける最適化の基本的な方法ですが、標準的な手法では 学習率の調整が難しい という問題があります。
この問題を解決するために、勾配降下法を改良した最適化アルゴリズム（Adam, RMSprop, Adagrad, Momentum など）が登場しました。

それぞれの手法は、学習をスムーズに進め、収束速度を向上させるために工夫が施されています。
ここでは、主要な高度な最適化手法について詳しく解説します。

1. Momentum（モーメンタム）

概要

モーメンタム（Momentum）とは、「勾配の過去の値を加味して更新する手法」 です。
通常の勾配降下法では、その都度勾配の方向に移動しますが、モーメンタムでは「前の移動方向を考慮して滑らかに更新」します。
これにより、勾配の変動が大きい場合でも、収束が速くなります。

更新式

$v_t = \beta v_{t-1} + (1 - \beta) \frac{\partial L}{\partial w}$ $w = w - \eta v_t$

特徴

✅ メリット

局所最適解に引っかかりにくくなる
振動が少なくなり、収束が安定する

⚠️ デメリット

学習率が適切でないと、逆に発散する可能性がある

➡ 一般的に、SGDと組み合わせて使用される（SGD + Momentum）

2. Adagrad（適応学習率勾配降下法）

概要

Adagrad（Adaptive Gradient Descent）とは、「パラメータごとに異なる学習率を設定する手法」 です。
通常の勾配降下法ではすべてのパラメータに同じ学習率を適用しますが、Adagradは「頻繁に更新されるパラメータの学習率を小さくし、あまり更新されないパラメータの学習率を大きくする」仕組みになっています。

更新式

$w = w - \frac{\eta}{\sqrt{G_t + \epsilon}} \frac{\partial L}{\partial w}$

ここで、

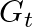$G_t$ は過去の勾配の二乗和
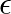$\epsilon$ はゼロ割を防ぐための微小値

特徴

✅ メリット

手動で学習率を調整しなくても良い
スパースなデータ（出現頻度が少ないデータ）に適している

⚠️ デメリット

学習率が徐々にゼロに近づくため、後半の学習が遅くなる

➡ 深層学習ではあまり使われなくなったが、一部のNLPタスクでは有効

3. RMSprop（Root Mean Square Propagation）

概要

RMSpropはAdagradの改良版 であり、学習率が徐々にゼロになってしまう問題を解決するために、勾配の二乗和の移動平均を取る 手法です。
これにより、学習が進んでも適切な学習率を維持できる ようになりました。

更新式

$E[g^2]<em>t = \beta E[g^2]</em>{t-1} + (1 - \beta) g_t^2$ $w = w - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \frac{\partial L}{\partial w}$

特徴

✅ メリット

過去の勾配の影響を適度に減らすため、学習率がゼロにならない
収束が速く、振動が少ない
畳み込みニューラルネットワーク（CNN）でよく使用される

⚠️ デメリット

ハイパーパラメータ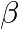（ $\beta$ ）の調整が必要

➡ CNN（畳み込みニューラルネットワーク）で広く使われる

4. Adam（Adaptive Moment Estimation）

概要

Adam（Adaptive Moment Estimation）は、「Momentum」と「RMSprop」を組み合わせた最適化手法」 です。
モーメンタムの「過去の勾配を考慮する性質」と、RMSpropの「適応的に学習率を調整する性質」を両方兼ね備えています。
現在、ディープラーニングで最もよく使われる最適化手法 です。

更新式

$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$ $v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$ $\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}$ $w = w - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t$

特徴

✅ メリット

学習率の調整が不要
収束が速い
ニューラルネットワークの訓練において最も広く使われる

⚠️ デメリット

一部の最適化問題（特に、シャープな最適解が必要な場合）では性能が落ちることがある

➡ 深層学習（特にTransformerやGANなどのモデル）で最も人気のある手法

5. 高度な最適化手法の比較

手法	特徴	メリット	デメリット	主な用途
Momentum	勾配の移動平均を考慮	局所最適を回避	学習率の調整が必要	SGDの改良
Adagrad	適応学習率	スパースデータに強い	学習率が小さくなりすぎる	NLPタスク
RMSprop	Adagradの改良	学習率がゼロにならない	ハイパーパラメータ調整が必要	CNN
Adam	Momentum + RMSprop	収束が速く、安定	一部のタスクでは最適でない	深層学習全般

6. まとめ

✅ 高度な最適化手法は、勾配降下法を改良し、学習をスムーズに進めるための手法
✅ Adamが最も広く使われ、CNNにはRMSpropも人気
✅ タスクに応じて、適切な手法を選択することが重要

ディープラーニングを実装する際は、基本的に「Adam」を使えばOK！ 🚀