単回帰分析とは – 生活と学びとプログラム

単回帰分析とは

単回帰分析とは、1つの説明変数（独立変数）を用いて、1つの目的変数（従属変数）を予測・説明するための統計的手法です。データ間の関係を直線で近似し、その関係性をモデル化することで、未来の予測や因果関係の把握に役立てることができます。

単回帰分析の目的
単回帰分析の目的で出てくる用語
単回帰分析を求める公式
単回帰分析のプロセス
具体例
- データセット
- 計算ステップ

まとめ
追加の学習リソース
以下、サンプルプログラム実装演習
サンプルプログラム演習問題
演習問題の解答
演習結果まとめ

単回帰分析の目的

単回帰分析の目的は以下の通りです：

関係性の把握
- 説明変数と目的変数の間にどのような関係があるかを定量的に示します。
- 例: 気温が上がるとアイスクリームの売上が増える関係。
予測
- 説明変数の値を使って、目的変数を予測します。
意思決定のサポート
- 分析結果を活用し、具体的な行動計画を立てます。
課題解決
- 問題をデータに基づいて数値的に捉え、解決に役立てます。

単回帰分析の目的で出てくる用語

1. 説明変数 (Explanatory Variable)

意味: 目的変数を説明するための変数。
例: 気温。

2. 目的変数 (Dependent Variable)

意味: 説明変数を用いて予測したい変数。
例: アイスクリームの売上。

3. 傾き (Slope)

意味: 説明変数が1単位増加したとき、目的変数がどの程度変化するかを表す値。

4. 切片 (Intercept)

意味: 説明変数が0のときの目的変数の値。

5. 決定係数 (R²)

意味: モデルがどの程度データを説明できているかを示す指標（1に近いほど良い）。

単回帰分析を求める公式

単回帰分析の基本式は以下の通りです。

回帰式

$y = ax + b$

y：目的変数
x：説明変数
a：傾き
b：切片

傾き a の計算式

$a = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}$

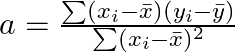
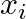$x_i$ ：各データポイントの説明変数
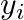$y_i$ ：各データポイントの目的変数
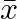$\bar{x}$ ：説明変数の平均値
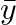$\bar{y}$ ：目的変数の平均値

切片 b の計算式

$b = \bar{y} - a \cdot \bar{x}$

単回帰分析のプロセス

データ収集
- 説明変数と目的変数のデータを収集します。
平均値の計算 　
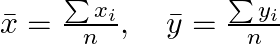
傾き a の計算　
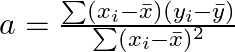
切片 b の計算 　
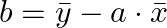
回帰式の作成

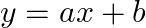
具体例

データセット

気温 (xx)	売上 (yy)
10	50
20	70
30	90

計算ステップ

平均値の計算 　
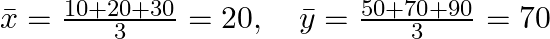
傾き a の計算 　
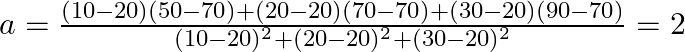
切片 b の計算　
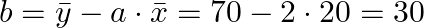
回帰式の作成 　
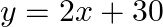
予測

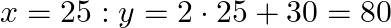
まとめ

単回帰分析は、1つの説明変数で目的変数を予測する手法。
Python では scikit-learn を使うと簡単に実装できる。
モデルの評価には決定係数 (R²) を活用する。

追加の学習リソース

以下、サンプルプログラム実装演習

単回帰分析の基本式は以下の通りです。
サンプルプログラムでは誤差を入れています。

$y = ax + b + \varepsilon$

y: 目的変数 (予測したい値)
x: 説明変数 (予測のためのデータ)
a: 回帰係数 (x の影響度)
b: 切片 (x=0 のときの y の値)
ε: 誤差 (予測できない要素)

1. データの準備

適当なデータを作成し、広告費と売上の関係を分析してみます。


import numpy as np
import matplotlib.pyplot as plt

# 乱数のシードを固定
np.random.seed(42)

# 広告費 (0〜10万円の範囲)
X = np.random.rand(50, 1) * 10

# 売上 (広告費に比例しつつノイズを含む)
y = 2.5 * X + np.random.randn(50, 1) * 2

# 散布図を描画
plt.scatter(X, y, color='blue', label="データ")
plt.xlabel("広告費 (万円)")
plt.ylabel("売上 (万円)")
plt.title("広告費と売上の関係")
plt.legend()
plt.show()

2. 線形回帰モデルの学習

Scikit-learn を使って、単回帰分析を実装します。


from sklearn.linear_model import LinearRegression

# モデルを作成
model = LinearRegression()

# 学習
model.fit(X, y)

# 回帰係数と切片を表示
print(f"回帰係数 (傾き): {model.coef_[0][0]:.2f}")
print(f"切片: {model.intercept_[0]:.2f}")

3. 予測と回帰直線の描画

モデルを使って予測し、回帰直線を描画します。


X_pred = np.linspace(0, 10, 100).reshape(-1, 1)  # 0~10 の範囲で100点のX値を作成
y_pred = model.predict(X_pred)  # 予測値

# 散布図 + 回帰直線
plt.scatter(X, y, color='blue', label="データ")
plt.plot(X_pred, y_pred, color='red', linewidth=2, label="回帰直線")
plt.xlabel("広告費 (万円)")
plt.ylabel("売上 (万円)")
plt.title("単回帰分析の結果")
plt.legend()
plt.show()

4. モデルの評価 (決定係数 R²)

モデルの精度を測るために、決定係数 (R²) を計算します。


from sklearn.metrics import r2_score

r2 = r2_score(y, model.predict(X))
print(f"決定係数 R²: {r2:.2f}")

サンプルプログラム演習問題

回帰モデルの傾き model.coef_ を手計算で求めてみよう。
データのノイズを増やして、R²の変化を観察してみよう。
広告費の範囲を 10 → 20 に変更すると、回帰直線はどう変化するか？

演習問題の解答

1. 回帰モデルの傾き `model.coef_` を手計算で求める

単回帰分析における回帰係数 (傾き) a は、以下の式で計算できます。 a=∑(Xi−Xˉ)(yi−yˉ)∑(Xi−Xˉ)2a = \frac{\sum (X_i – \bar{X})(y_i – \bar{y})}{\sum (X_i – \bar{X})^2}

手順：

X の平均 を求める: Xˉ\bar{X}
y の平均 を求める: yˉ\bar{y}
分子を計算: 各 (X_i - X̄) * (y_i - ȳ) を合計
分母を計算: 各 (X_i - X̄)^2 を合計
傾き a を求める: 分子 ÷ 分母

Python コードで計算

# Xとyの平均
X_mean = np.mean(X)
y_mean = np.mean(y)

# 分子: (X - X_mean) * (y - y_mean) の総和
numerator = np.sum((X - X_mean) * (y - y_mean))

# 分母: (X - X_mean)^2 の総和
denominator = np.sum((X - X_mean) ** 2)

# 傾き a (回帰係数)
a_manual = numerator / denominator

print(f"手計算の回帰係数: {a_manual:.2f}")
print(f"Scikit-learn の回帰係数: {model.coef_[0][0]:.2f}")

結果

model.coef_ の値と 同じ結果 になるはずです。

2. データのノイズを増やして、R²の変化を観察する

ノイズを増やすことで、データのばらつきが増加し、モデルの精度 (R²) が変化します。
以下のコードを使って、ノイズを 2 → 5 に変更した場合の影響を観察できます。

# ノイズを増やす
y_noisy = 2.5 * X + np.random.randn(50, 1) * 5  # 標準偏差を 5 に変更

# 新しい回帰モデルの学習
model_noisy = LinearRegression()
model_noisy.fit(X, y_noisy)

# R² を計算
r2_noisy = r2_score(y_noisy, model_noisy.predict(X))

print(f"元の R²: {r2:.2f}")
print(f"ノイズを増やした後の R²: {r2_noisy:.2f}")

予想される結果：

元の R² (例: 0.90)
ノイズ増加後の R² (例: 0.65) → 精度が下がる

結論：

ノイズが増えるとデータが散らばる ため、回帰直線が当てはまりにくくなる。
その結果、決定係数 (R²) が低下し、モデルの精度が下がる。

3. 広告費の範囲を `10 → 20` に変更すると、回帰直線はどう変化するか？

結論：

広告費 X の範囲を 10 → 20 に変更しても、回帰直線の傾きは変わらない。
しかし、X の最大値が変わることで、回帰直線のスケール (x軸の範囲) が変化する。

以下のコードで、広告費 X を 0~20 の範囲に変更してみます。

# X を 0~20 の範囲に変更
X_expanded = np.random.rand(50, 1) * 20
y_expanded = 2.5 * X_expanded + np.random.randn(50, 1) * 2

# 新しい回帰モデル
model_expanded = LinearRegression()
model_expanded.fit(X_expanded, y_expanded)

# 予測値
X_pred_expanded = np.linspace(0, 20, 100).reshape(-1, 1)
y_pred_expanded = model_expanded.predict(X_pred_expanded)

# プロット
plt.scatter(X_expanded, y_expanded, color='blue', label="データ")
plt.plot(X_pred_expanded, y_pred_expanded, color='red', linewidth=2, label="回帰直線")
plt.xlabel("広告費 (万円)")
plt.ylabel("売上 (万円)")
plt.title("広告費の範囲を 10 → 20 に変更した場合")
plt.legend()
plt.show()

変化点

回帰直線の傾き (model.coef_) は変わらない。
X の範囲が拡大するので、回帰直線の長さが伸びる。
しかし、モデルの精度 (R²) には大きな影響はない。

演習結果まとめ

問題	結果・ポイント
1. 傾きを手計算	`model.coef_` の公式を使って、手計算可能
2. ノイズ増加	`R²` (決定係数) が低下し、精度が下がる
3. 広告費の範囲変更	傾きは変わらず、回帰直線のスケールだけ変化