活性化関数（Sigmoid, tanh, ReLU, Softmax）

ニューラルネットワークでは、活性化関数は各ニューロンの出力を変換し、学習の進行を助ける重要な要素です。ここでは代表的な 4つの活性化関数（シグモイド関数、tanh関数、ReLU関数、Softmax関数） について説明します。

1. シグモイド関数（Sigmoid Function）

定義

$\sigma(x) = \frac{1}{1 + e^{-x}}$

特徴

出力範囲：(0,1)(0, 1)
確率的な出力を求める場合に適している
小さな値は0に、大きな値は1に近づく
微分可能な非線形関数

欠点

勾配消失問題（Vanishing Gradient Problem）
大きな入力値（正または負）の場合、勾配が極めて小さくなり、ニューラルネットワークの学習が進みにくくなる。
ゼロ中心でない（Not Zero-Centered）
出力の範囲が 00 から 11 なので、重みの更新が一方向に偏りやすくなる。

適用例

ロジスティック回帰
出力層が2クラス分類（バイナリー分類）の場合

2. tanh（双曲線正接）関数

定義

$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

特徴

出力範囲：(−1,1)(-1, 1)
シグモイド関数よりもゼロ中心（Zero-Centered）であるため、学習が速くなる
非線形かつ微分可能

欠点

勾配消失問題：シグモイド関数と同様に、値が極端に大きいと勾配が小さくなる

適用例

隠れ層（Hidden Layer）の活性化関数としてよく使われる
特に、ゼロを中心とした入力データを扱う場合に有効

3. ReLU（Rectified Linear Unit）関数

定義

$f(x) = \max(0, x)$

特徴

出力範囲：[0,∞)[0, \infty)
勾配消失問題を軽減
負の値の勾配がゼロになるが、正の値はそのまま伝播されるため、学習が速くなる
計算コストが低く、ディープラーニングで広く使用される

欠点

死んだReLU（Dead Neuron Problem）
負の入力を受けると、そのニューロンの勾配が0になり、学習が停止する。
ゼロ中心でない
出力が0以上であるため、学習がやや非効率になる可能性がある。

適用例

CNN（畳み込みニューラルネットワーク）やDNN（深層ニューラルネットワーク）の隠れ層で主流の活性化関数
画像認識などの分野で頻繁に使用される

4. Softmax関数

定義

Softmax関数は、多クラス分類問題（3クラス以上の分類）における出力層でよく使用される活性化関数です。
KK 個の出力を持つニューラルネットワークにおいて、各クラス ii の確率を次のように計算します。

$\sigma(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{K} e^{x_j}}$

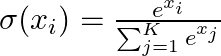
特徴

出力範囲：(0,1)(0, 1)
すべての出力の合計が1になるため、確率分布として解釈できる
各ニューロンの出力を相対的にスケール変換する

欠点

指数関数を使うため計算コストが高い
勾配消失の可能性：大きな入力値と小さな入力値の差が極端な場合、特定のクラスの勾配が極端に小さくなることがある。

適用例

**多クラス分類（Multi-Class Classification）**の出力層
画像分類タスク（例：手書き数字認識のMNIST）

比較表

活性化関数	出力範囲	ゼロ中心	勾配消失問題	主な用途
Sigmoid	(0,1)(0,1)	✗（なし）	あり	出力層（確率）
tanh	(−1,1)(-1,1)	✓（あり）	あり	隠れ層（一般的）
ReLU	[ 0, ∞ ]	✗（なし）	なし（Dead ReLUの問題あり）	隠れ層（深層学習）
Softmax	(0,1)(0,1)	✗（なし）	あり（大きな差があると影響大）	出力層（多クラス分類）

まとめ

✅ シグモイド関数 は確率的な出力を求める場合に有効だが、勾配消失問題がある。
✅ tanh関数 はシグモイドより学習が進みやすいが、やはり勾配消失のリスクがある。
✅ ReLU関数 は計算コストが低く、勾配消失の問題を軽減するため、ディープラーニングで広く使われる。
✅ Softmax関数 は多クラス分類の出力層で最適だが、指数関数を含むため計算コストが高い。

現在の深層学習では、
✅ 隠れ層には ReLU
✅ 出力層には用途に応じた関数（Sigmoid, Softmaxなど）
を使うのが一般的です。