目次
線形代数とは?
1. 線形代数の概要
線形代数(Linear Algebra)は、ベクトルや行列を用いた数学の分野であり、 データ解析、機械学習、物理学、コンピュータグラフィックス など、幅広い分野で活用されています。
線形代数は、次のような概念を中心に扱います。
- ベクトル(向きと大きさを持つ量)
- 行列(数値を格子状に配置したもの)
- 線形写像(ベクトル空間の変換)
- 固有値・固有ベクトル(行列の特性を示す指標)
この知識を活用すると、回帰分析やニューラルネットワーク などの機械学習モデルの理解が深まります。
2. 線形代数の基本的な公式
(1) ベクトルの内積
![]()
内積は、2つのベクトルの相関や角度を計算する際に用いられます。
(2) 行列の積
![]() の場合、行列
の場合、行列 ![]() と
と ![]() の積は、次のように計算されます。
の積は、次のように計算されます。
![]()
行列の積は、変換やデータ処理に頻繁に用いられます。
(3) 行列の逆行列
逆行列 ![]() は、次の関係を満たします。
は、次の関係を満たします。
![]()
ここで ![]() は単位行列です。
は単位行列です。
3. 線形代数の応用
(1) 機械学習における応用
- 回帰分析(線形回帰・重回帰分析)
- 主成分分析(PCA)(データの次元削減)
- ニューラルネットワーク(行列演算を活用)
(2) 物理学・エンジニアリングにおける応用
- 力学シミュレーション(ベクトル演算)
- 電磁気学(行列を使った場の解析)
(3) コンピュータグラフィックス(CG)
- 3D変換(拡大・回転・移動)
- 光の反射や陰影の計算
4. 線形代数まとめ
- 線形代数は、ベクトルや行列を用いた数学であり、多くの分野で活用されている。
- 機械学習やデータ解析において、基礎となる概念を提供する。
- 具体的な応用として、回帰分析、PCA、ニューラルネットワーク などがある。
5. 転置行列・単位行列・逆行列
転置行列(Transpose)
行列 AA の転置とは、行と列を入れ替えた行列のことを指します。
例えば、行列 AA が以下のような場合:
![]()
その転置行列 ATA^T は、
![]()
となります。転置は、内積計算や対称行列の性質を利用する際に重要になります。
単位行列(Identity Matrix)
単位行列とは、対角成分がすべて1で、それ以外の成分が0である正方行列です。
例えば、3×3の単位行列は以下のようになります:
![]()
単位行列は、行列の積において乗法単位元の役割を果たし、どんな行列 AA に対しても、
![]()
となります。
逆行列(Inverse Matrix)
逆行列とは、ある行列 AA に対して、別の行列 A−1A^{-1} を掛けたときに単位行列 II となる行列のことを指します。
![]()
例えば、2×2行列の逆行列は以下のように計算できます:
![]()
の逆行列は、
![]()
ただし、行列の行列式(determinant) ![]() が0でない場合に限ります。
が0でない場合に限ります。
ベクトルで微分
ベクトル・行列を用いた微分では、スカラー関数 ![]() をベクトル
をベクトル ![]() に対して微分する操作がよく用いられます。例えば、
に対して微分する操作がよく用いられます。例えば、
![]()
のような式の微分を求める際、線形代数の知識が必要です。
具体的には、![]() の場合、微分は
の場合、微分は
![]()
となります。特に ![]() が対称行列の場合、結果は
が対称行列の場合、結果は ![]() となります。
となります。
重回帰分析でこれらが必要な理由
重回帰分析では、複数の説明変数 ![]() を用いて目的変数
を用いて目的変数 ![]() を予測するため、行列計算が必要になります。
を予測するため、行列計算が必要になります。
最小二乗法による回帰係数の求め方は以下のようになります:
![]()
ここで、各線形代数の概念がどのように関係するか説明します。
- 転置行列
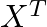 は設計行列
は設計行列 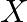 の転置行列であり、回帰係数の計算時に必要。
の転置行列であり、回帰係数の計算時に必要。- 内積計算や共分散行列の計算に使われる。
- 単位行列
- 逆行列を求める際に、単位行列を用いることがある。
- 正則化(リッジ回帰など)を行う際に、単位行列を追加して安定化を図ることがある:
![]()
逆行列
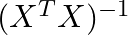 の計算によって、最小二乗法の解が得られる。
の計算によって、最小二乗法の解が得られる。- 逆行列が存在しない場合(行列が特異である場合)は、擬似逆行列を使う。
ベクトルで微分
- 最小二乗法では、誤差関数を微分して最適解を求めるため、行列微分の知識が必要。
- 誤差関数
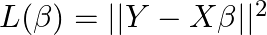 を最小化するために、
を最小化するために、
![]()
となり、回帰係数の公式が導かれる。
6.転置・行列 まとめ
- 転置行列 は回帰係数の計算や内積に利用。
- 単位行列 はリッジ回帰などの正則化に利用。
- 逆行列 は最小二乗法の解を求めるために必要。
- ベクトルの微分 は最適化問題を解く際に必要。
7. 関連ページ
線形代数を基盤とする回帰分析の詳細については、以下のページをご覧ください。