重回帰分析

重回帰分析とは？

1. 重回帰分析の概要

重回帰分析（Multiple Linear Regression）は、複数の説明変数（独立変数） を用いて 目的変数（従属変数） を予測する統計的手法です。

単回帰分析では1つの説明変数しか扱いませんが、重回帰分析では複数の変数を考慮できるため、より精度の高い予測やデータの関係性の分析が可能になります。

2. 重回帰分析の公式

重回帰分析の数学的表現は次のようになります。

$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_n + \varepsilon$

各変数の意味

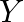$Y$ ：目的変数（予測したい値）
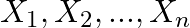$X_1, X_2, ..., X_n$ ：説明変数（予測に用いるデータ）
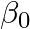$\beta_0$ ：切片（回帰直線のy切片）
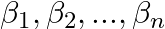$\beta_1, \beta_2, ..., \beta_n$ ：回帰係数（各説明変数の影響度を示す）
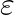$\varepsilon$ ：誤差項（モデルが説明できないランダムな変動）

この式を使い、データの関係性をモデル化し、新しいデータに対して予測を行います。

3. 重回帰分析の目的

(1) 予測

重回帰分析は、複数の要因が関係するケースで将来の結果を予測するために使用されます。

例：

住宅価格の予測（面積、部屋数、立地などの変数を使用）
売上の予測（広告費、季節要因、過去の売上データを考慮）

(2) 要因の分析

どの説明変数が目的変数にどれだけ影響を与えるかを数値的に把握できます。

例：

従業員の生産性 を決定する要因（労働時間、経験年数、教育レベル）
患者の病気のリスク に影響を与える要因（食習慣、運動量、遺伝）

(3) 因果関係の検証

ある変数が目的変数にどの程度影響を与えるかを調べる。
マーケティングの効果分析 などに応用される。

4. 重回帰分析のプロセス

(1) データの準備

目的変数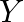（ $Y$ ）と説明変数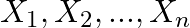（ $X_1, X_2, ..., X_n$ ）を定義する。
外れ値や欠損値を確認し、必要に応じて処理する。

(2) モデルの構築

最小二乗法（OLS: Ordinary Least Squares）を用いて回帰係数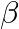（ $\beta$ ）を求める。
OLSは、誤差の二乗和を最小化 するように係数を決定する。

(3) モデルの評価

決定係数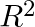（ $R^2$ ）：モデルの予測精度を評価する。
p値（有意性検定）：説明変数が統計的に有意かどうかを判定する。
残差分析：誤差の傾向を分析し、正規性や均一性を確認する。

(4) 予測の実施

訓練データで学習したモデルを用いて、新しいデータに対する予測を行う。

(5) モデルの改善

説明変数の選択を最適化する。
過学習を防ぐため、Lasso回帰やRidge回帰を活用することもある。

5. 具体例：住宅価格の予測

問題設定

ある地域の住宅価格（ $Y$ ）を以下の説明変数を用いて予測する。

ID	面積（ $X_1$ ）	部屋数（ $X_2$ ）	築年数（ $X_3$ ）	価格（ $Y$ ）
1	80	3	5	3000
2	100	4	10	4000
3	60	2	3	2500

モデルの構築

重回帰分析の式は以下のようになる：

$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \varepsilon$

このモデルをデータにフィットさせ、 $\beta$ を求めることで、新しい住宅の価格を予測できる。

6. 専門用語の説明

独立変数（説明変数）：目的変数を予測するために使用する変数。
従属変数（目的変数）：予測したい変数。
回帰係数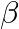（ $\beta$ ）：説明変数の影響度を示すパラメータ。
最小二乗法（OLS）：誤差を最小化するための方法。
決定係数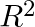（ $R^2$ ）：モデルの予測力を評価する指標。
多重共線性：説明変数同士の相関が高すぎる場合に発生し、適切な回帰分析を妨げる問題。

7. まとめ

重回帰分析は、複数の変数を用いて結果を予測する強力な手法。
予測、要因分析、因果関係の検証に利用される。
機械学習やデータサイエンスの基礎となる数学的アプローチ であり
Pythonのライブラリ（Scikit-learn, Statsmodels） などを活用すると簡単に実装可能になる。

8. 重回帰分析の実装

重回帰分析は、複数の変数を用いて結果を予測する強力な手法。
予測、要因分析、因果関係の検証に利用される。