目次
線形回帰の概要
1. 線形回帰とは（導入）
線形回帰は、入力変数（特徴量）と出力変数（目的変数）の関係を直線でモデル化する回帰手法 です。
これは、機械学習・統計学の基本的なモデルであり、多くの応用分野で使われます。
数学的には、線形代数を活用してモデルを求める ことが多く、データの傾向を理解し予測するための基礎となります。
2. 線形回帰の数式と基礎
単回帰分析（Simple Linear Regression）
単回帰分析では、説明変数が1つのとき、次のように表現されます：
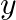：目的変数（予測する値）
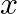：説明変数（特徴量）
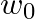：切片（intercept）
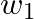：回帰係数（重み）
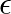：誤差項（residual error）
重回帰分析（Multiple Linear Regression）
説明変数が複数ある場合、数式は次のようになります：
このように、複数の特徴量（変数）を考慮することで、より複雑な関係を表現できます。
3. 線形代数との関係
線形回帰は、行列を用いた計算によって求めることができます。
行列表現
行列形式で表すと、以下のように記述できます：
ここで：
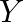：目的変数のベクトル
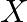：説明変数の行列
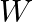：回帰係数のベクトル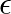- ：誤差ベクトル
最小二乗法（Least Squares Method）
最小二乗法を使うと、回帰係数 は次のように求められます：
この計算により、誤差を最小化する最適な回帰係数を求めることができます。
4. 線形回帰の種類
単回帰分析（Simple Linear Regression）
- 説明変数が1つの回帰分析。
- 直線の傾きを求め、データの傾向を分析。
重回帰分析（Multiple Linear Regression）
- 説明変数が複数ある回帰分析。
- 例えば、不動産価格の予測に「面積・立地・築年数」を組み合わせて使う。
正則化回帰（Ridge/Lasso Regression）
- 過学習を防ぐための手法。
- リッジ回帰（Ridge Regression）：L2正則化
- ラッソ回帰（Lasso Regression）：L1正則化
5. 応用と事例
- ビジネス・マーケティング → 広告費と売上の関係を予測
- 医療 → 患者データから病気の発症リスクを予測
- 経済 → GDPの予測、株価予測