行列の操作 – 生活と学びとプログラム

行列演算の基礎
まとめ

行列演算の基礎

行列演算は機械学習、画像処理、音声解析などさまざまな分野で使われる。特に、音声解析では スペクトログラム変換、特徴量抽出、行列分解（SVDなど） などで頻繁に使用される。

行列演算の種類

行列演算は以下のようなプロセスで利用される。

ベクトル・行列の定義
転置（Transpose）
行列の逆行列（Inverse Matrix）
行列積（Matrix Multiplication）
行列の正規化（Normalization）
特異値分解（Singular Value Decomposition, SVD）
主成分分析（Principal Component Analysis, PCA）

1. ベクトル・行列の定義

ベクトルや行列を定義することで、後の演算を可能にする。

import numpy as np

# ベクトルの定義
x = np.array([
    [1],
    [2],
    [3]
])
print(x)

$x = \begin{bmatrix} 1 \ 2 \ 3 \end{bmatrix}$

2. 転置（Transpose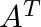）: ( $A^T$ )

行列の行と列を入れ替える。

X = np.array([
    [1, 2],
    [3, 4]
])
Xt = X.T
print(Xt)

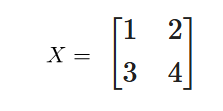
用途

音声特徴量の行列変換
機械学習のデータ前処理
行列積計算の準備

3. 行列の逆行列（Inverse Matrix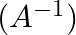）: $( A^{-1} )$

逆行列を求めることで、方程式の解を得る。

X_inv = np.linalg.inv(X)
print(X_inv)

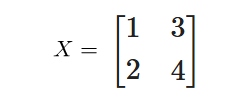
用途

線形方程式の解決（音声フィルタ処理）
音声信号処理におけるフィルタ設計
正則化を利用した信号ノイズ除去

4. 行列積（Matrix Multiplication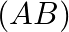）: $(AB)$

行列の掛け算を行い、特徴抽出や変換を行う。

XX_inv = np.dot(X, X_inv)
print(XX_inv)

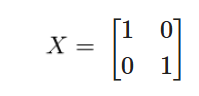
用途

信号変換（フィルタ処理）
データ圧縮（PCA, SVD）
音声解析での時間周波数変換

5. 行列の正規化（Normalization）

数値スケールを 0-1 に調整することで計算の安定性を向上させる。

A_norm = (X - np.min(X)) / (np.max(X) - np.min(X))
print(A_norm)

$A_{\text{norm}} = \frac{A - \min(A)}{\max(A) - \min(A)}$

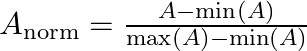
用途

データの前処理
スペクトログラムのスケーリング
ニューラルネットワークの入力処理

6. 特異値分解（Singular Value Decomposition, SVD）

行列を分解し、次元削減や特徴抽出に使う。

U, S, Vt = np.linalg.svd(X)
print(U, S, Vt)

$A = U \Sigma V^T$

用途

音声特徴抽出（MFCC, LPC）
次元削減（PCA）
データ圧縮

7. 音声解析の処理フロー

音声解析における行列演算の順序

音声信号の取得（WAV, MP3 など）
フーリエ変換（FFT）で周波数成分に変換
スペクトログラム生成（STFT）
行列の転置・正規化
MFCC などの特徴抽出
次元削減（SVD, PCA）
分類モデルや機械学習アルゴリズムへ入力

まとめ

行列演算は音声解析や機械学習で不可欠な要素であり、特に以下の流れで使われる。

転置（Transpose） → データ構造を変える
逆行列（Inverse Matrix） → 方程式の解を求める
行列積（Matrix Multiplication） → 信号変換やフィルタ処理
特異値分解（SVD） → 特徴抽出や次元削減