目次
転置(Transpose)とは?
転置とは、行列の行と列を入れ替える操作 である。転置を行うことでデータ構造を変え、計算の利便性を向上させることができる。特に、機械学習、音声解析、画像処理 などの分野で頻繁に使用される。
1. 転置の基本
行列 AA の転置を ATA^T と表す。これは行列の各要素の位置を 行と列を入れ替える ことで求められる。
例1:ベクトルの転置
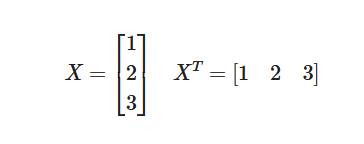
例2:行列の転置
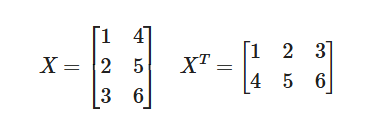
このように、各要素の位置を交換することで転置行列が得られる。
2. 転置の公式
転置にはいくつかの基本的な性質がある。これらは、行列の演算を行う際に重要なルールとなる。
二重転置(元の行列に戻る)
![]()
積の転置(順番が逆になる)
![]()
3つの行列の積の転置
![]()
この法則は、行列計算の際に演算順序を変えずに転置を適用するために不可欠である。
3. 転置を用いるデータ構造の変換
転置は、様々なデータ構造を変えるために使用される。以下の例は、機械学習や音声処理での活用法を示す。
(1) データの行列形式を変更
データセットを行ベクトルから列ベクトルに変換する場合、転置を用いることで計算のしやすさが向上する。
例えば、特徴量ベクトルが行ベクトルの形で与えられている場合、ニューラルネットワークの入力に適した形(列ベクトル)に変換できる。
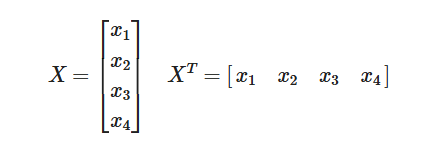
(2) 行列演算の整合性を保つ
例えば、行列 A と B の積 AB が計算できない場合、転置を利用して適切な形に変形することができる。
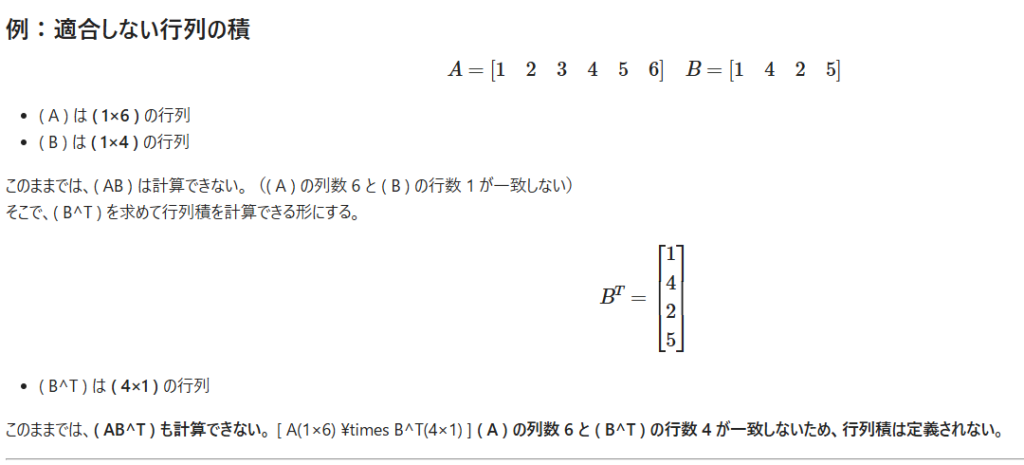

(3) 音声解析における転置の利用
音声データを分析する際、スペクトログラムの生成 や 特徴量の整理 に転置を用いることがある。
スペクトログラム
時間と周波数の情報を持つ スペクトログラム は、通常 時間(フレーム)×周波数(バンド) の形で表現される。
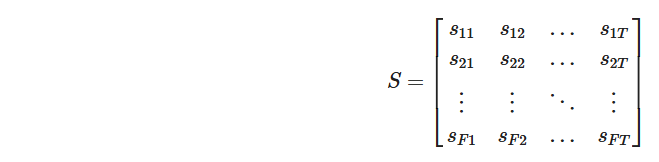
これを転置することで、周波数ごとに時間変化を解析しやすくすることができる。
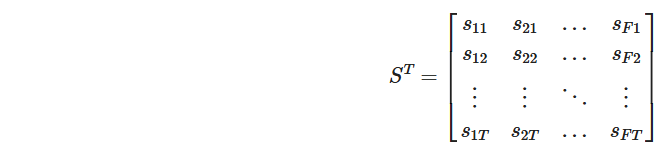
この操作により、時間系列データを周波数ベースで分析しやすくなる。
4. 転置のPython実装
Python(NumPy)を使えば、転置は簡単に行える。
import numpy as np
# 行列の定義
A = np.array([
[1, 2, 3],
[4, 5, 6]
])
# 転置の適用
A_T = A.T
# 出力
print(A_T)
出力:
[[1 4]
[2 5]
[3 6]]
5. まとめ
転置は、データの形式を変えたり、計算を適合させたりするために重要な操作である。
- 行列の転置とは、行と列を入れ替えること
- 転置の公式(積の順序が逆転するなど)は重要
- データの形を変えることで、機械学習や音声解析に活用できる
- 音声解析では、スペクトログラムの解析に転置を利用する
- Python(NumPy)を使えば簡単に転置を実装可能
このように、転置は様々な分野で活用できる、理解できれば把握に役に立つ。