単位行列と逆行列

単位行列とは

単位行列（Identity Matrix）とは、対角成分がすべて 1 で、それ以外が 0 である正方行列のことを指します。
これは、スカラーの「1」に相当し、任意の行列

AA に対して以下の関係が成り立ちます。

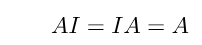
例えば、次のような形の行列です：


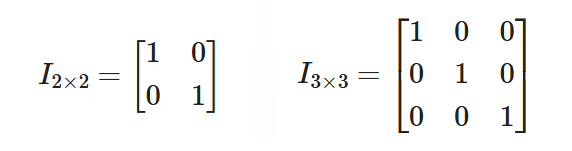
単位行列の応用

単位行列は、以下のような場面で利用されます。

  • 行列の乗算の単位元として機能（スカラーの “1” に相当）
  • 逆行列を求める際の基準（ガウス・ジョルダン法などで利用）
  • リッジ回帰などの正則化手法
    例えば、回帰分析で正則化を行う場合、単位行列を加えることで計算の安定性を向上させる：

\hat{\beta} = (X^T X + \lambda I)^{-1} X^T Y


行列の積と単位行列

例えば、次のような行列 A があるとします。

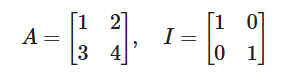
このとき、行列積を計算すると、

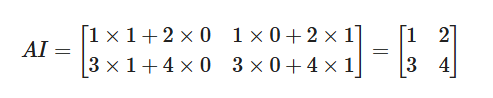
したがって、単位行列を掛けても元の行列 AA が変わらないことが確認できます。


逆行列とは？

逆行列（Inverse Matrix）とは、ある行列 AA に対して、以下の関係を満たす行列 A−1A^{-1} のことを指します。

A A^{-1} = A^{-1} A = I

これは、スカラーにおける逆数（例えば 2 × 12\frac{1}{2} = 1 ）に相当する概念です。


逆行列の求め方（2×2行列）

2×2行列の逆行列は、行列の 行列式（determinant） を用いて次のように計算できます。

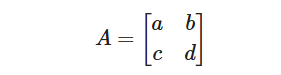
このとき、逆行列 A−1A^{-1} は

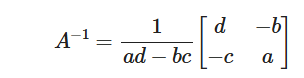
ただし、行列式 det⁡(A)=ad−bc\det(A) = ad – bc が 0 でない場合に限ります。


2×2行列の逆行列計算

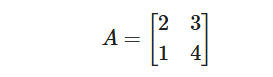
行列式（determinant）を計算すると、

\det(A) = 2 \times 4 - 3 \times 1 = 8 - 3 = 5

したがって、逆行列 A−1A^{-1} は、

A^{-1} = \frac{1}{5} \begin{bmatrix} 4 & -3 \ -1 & 2 \end{bmatrix} = \begin{bmatrix} \frac{4}{5} & -\frac{3}{5} \ -\frac{1}{5} & \frac{2}{5} \end{bmatrix}

このようにして、逆行列を求めることができます。


逆行列が存在しない場合

  • 行列が 特異行列（Singular Matrix） である場合、つまり 行列式が 0 の場合、逆行列は存在しません。
  • そのような場合、擬似逆行列（Moore-Penrose Pseudoinverse） を使って近似的に逆行列を求めます。

まとめ

  • 単位行列 II は、行列の「1」に相当し、行列を変えずに掛け算ができる。
  • 逆行列 A−1A^{-1} は、行列の「逆数」に相当し、掛けると単位行列になる。
  • 逆行列は、行列式が 0 でないときにのみ求めることができる。
  • 特異行列の場合、擬似逆行列を用いることがある。