線形代数とは
線形代数は、ベクトルや行列を扱う数学の分野であり、機械学習やデータ分析、物理学など幅広い分野で活用されます。特に機械学習においては、データの処理やモデルの計算において不可欠な要素となります。
このページでは、線形代数に関連する重要なトピックについて説明し、詳細な解説ページへのリンクを掲載します。また、数学的な公式や理論的な背景も含め、より深い理解を得られるように構成しました。
数学的な背景と公式
線形代数の理解には、以下のような数学的概念と公式が重要です。
1. 行列の基本演算
- 行列の加算・減算：要素ごとの演算
- 行列の乗算：内積を利用した計算
- 転置行列：行と列を入れ替える操作
- 逆行列：正則行列のみに存在し、線形方程式の解に使用
2. 固有値と固有ベクトル
- 固有値
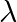と固有ベクトル 
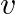は、行列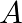 
に対して以下の関係を満たす：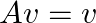
- これらは、機械学習の主成分分析（PCA）などで活用される。
3. 線形方程式の解法
- 連立一次方程式の行列表現
- ガウス消去法、クラメールの公式などの解法
より詳しい理論的背景については、以下のページをご覧ください。
➡ 線形回帰の概要
各トピックの概要
行列の操作
行列の操作は、線形代数の基本となる概念であり、行列の加算、乗算、転置、逆行列などの計算を指します。機械学習では、データの前処理や重みの更新に頻繁に使用されます。
詳しくは以下のページをご覧ください。
➡ 行列の操作
単回帰分析
単回帰分析は、説明変数が1つだけの回帰分析手法です。これは、ある変数（独立変数）が別の変数（従属変数）にどのように影響を与えるかを分析するために用いられます。例えば、広告費と売上の関係を調べる際に使用されます。
詳しくは以下のページをご覧ください。
➡ 単回帰分析
重回帰分析
重回帰分析は、説明変数が複数ある回帰分析手法です。これは、複数の要因が結果にどのように影響を与えるかを分析するのに適しており、不動産価格の予測やマーケティングデータの分析などに活用されます。
詳しくは以下のページをご覧ください。
➡ 重回帰分析
このページでは、線形代数に関連する基本的な概念について簡単に紹介しました。各トピックの詳細な解説については、リンク先のページを参考にしてください。