Categorical Crossentropy とは？

Categorical Crossentropy とは？

categorical_crossentropy（カテゴリカル交差エントロピー）は、多クラス分類（one-hot エンコーディングされたラベル）に使用される損失関数です。

1. categorical_crossentropy の定義

categorical_crossentropy は、モデルの出力確率と正解ラベルの確率分布の差を測る損失関数です。

$L = -\sum_{i=1}^{C} y_i \log(\hat{y}_i)$

各変数の意味：

$C$ ：クラスの数
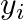$y_i$ ：正解ラベル（one-hot ベクトル）
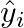$\hat{y}_i$ ：予測確率（Softmax の出力）
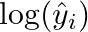$\log(\hat{y}_i)$ ：予測確率の対数

この数式では、正解クラスの確率の対数を取って負の和を計算 することで、予測がどれだけ間違っているかを評価します。

2. categorical_crossentropy の特徴

✅ 多クラス分類の損失関数として使用
✅ one-hot エンコーディングされたラベルと組み合わせる
✅ Softmax の出力を確率として利用する
✅ 正解に近い予測ほど損失が小さくなる

3. categorical_crossentropy の計算例

(1) ラベルと予測確率

4クラス分類の例を考えます。

正解ラベル（one-hot エンコーディング） y = [0, 1, 0, 0]
ニューラルネットワークの出力（Softmax の確率） \hat{y} = [0.1, 0.7, 0.1, 0.1]

(2) categorical_crossentropy の計算

$L = - \left( 0 \times \log 0.1 + 1 \times \log 0.7 + 0 \times \log 0.1 + 0 \times \log 0.1 \right)$

$L = - \log 0.7$

$L = 0.3567$

✅ 予測確率 0.7 が 1 に近いため、損失は比較的小さくなります。

4. categorical_crossentropy と sparse_categorical_crossentropy の違い

項目	categorical_crossentropy	sparse_categorical_crossentropy
ラベルの形式	One-hot エンコーディング（例：`[0, 1, 0, 0]`）	整数ラベル（例：`1`）
使用ケース	ラベルが one-hot の場合	ラベルが整数のカテゴリ番号の場合
計算方法	すべてのクラスの対数を考慮	正解クラスの対数のみ計算

✅ どちらを使うべきか？

ラベルが one-hot → categorical_crossentropy
ラベルが整数（0,1,2,…） → sparse_categorical_crossentropy

5. categorical_crossentropy の Keras 実装例

Keras では、categorical_crossentropy を損失関数として簡単に指定できます。

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Softmax
from tensorflow.keras.losses import categorical_crossentropy
from tensorflow.keras.optimizers import Adam

# モデルの作成
model = Sequential([
    Dense(64, activation='relu'),
    Dense(4, activation='softmax') # 4クラス分類
])

# モデルのコンパイル
model.compile(optimizer=Adam(), loss=categorical_crossentropy, metrics=['accuracy'])

# one-hot エンコーディングされたラベルのデータを使って学習
model.fit(x_train, y_train, epochs=10, batch_size=32)

6. categorical_crossentropy を使用する際のポイント

Softmax 関数の出力とセットで使用する
ラベルは one-hot エンコーディングされている必要がある
ラベルが整数なら sparse_categorical_crossentropy を使う
確率の高いクラスほど損失が小さくなる
予測が間違っているほど損失が大きくなる

7. まとめ

項目	内容
目的	多クラス分類の損失関数
数式	$L = -\sum_{i=1}^{C} y_i \log(\hat{y}_i)$
入力	Softmax の出力（確率）
ラベル	One-hot エンコーディング
類似関数	`sparse_categorical_crossentropy`（整数ラベル用）
Keras での指定	`loss='categorical_crossentropy'`