目次
微分・偏微分
微分の基礎知識
① 微分の目的
微分とは、変化率を求めるための数学的手法です。日常生活や自然現象において、次のような目的で使われます:
変化の速さを調べる
・例: 車が移動する速度(距離の時間に関する変化)を求める。
最適化(最大値・最小値)を探す
・例: 会社の利益を最大化する価格を計算する。
グラフの形状を理解する
・例: 曲線の傾きや極値(山や谷)を調べる。
② 微分の公式・用途
微分を計算するための公式を一覧にまとめます。
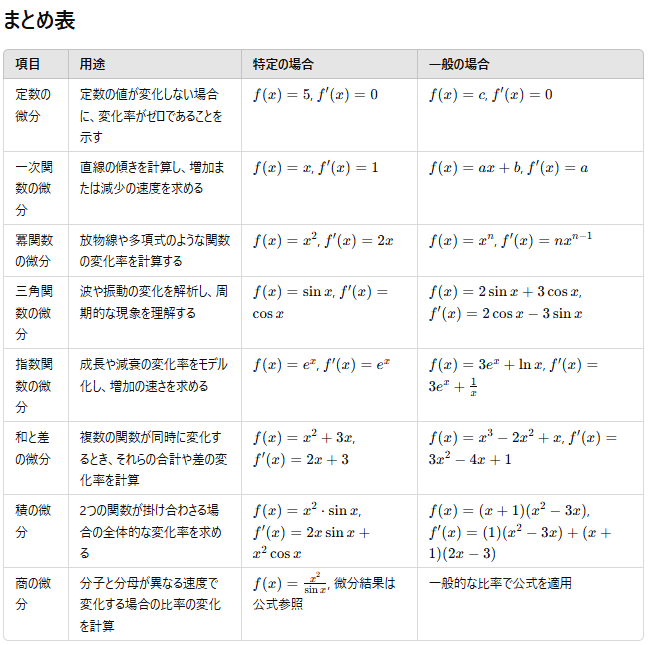
1. 定数の微分

2. 一次関数の微分

3. 冪関数の微分

4. 三角関数の微分

5. 指数関数と対数関数の微分

6. 和と差の微分

7. 積の微分(積の法則)

8. 商の微分(商の法則)

③ その他の知識(偏微分)
偏微分とは?
偏微分は、複数の変数を持つ関数に対して、一つの変数だけを変化させたときの変化率を計算する方法です。他の変数は固定されていると考えます。
例えば、関数 f(x, y) が x と y の2つの変数に依存するとき、x だけを変化させたときの変化率を偏微分によって求めます。
公式
- 偏微分の定義
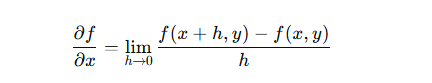
ここで、y は固定されており、x のみを変化させます。
- 多変数関数の偏微分
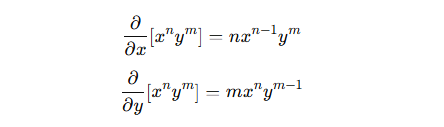
偏微分では、微分していない変数を定数として扱います。
用途
1. 複数要因の影響を解析する
偏微分は、複数の要因が関数に影響を与える場合に、それぞれの要因がどの程度結果に影響するかを解析するために使われます。
例: 経済学で生産量 Q が労働 L と資本 K に依存する場合、
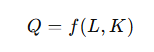
偏微分を使うと、以下のようにそれぞれの要因が生産量に与える影響を解析できます:
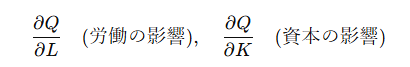
2. 勾配(傾き)の計算
偏微分は、3Dグラフ上のある点での傾き(勾配)を求めるのに使います。
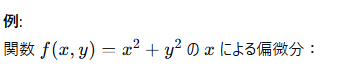
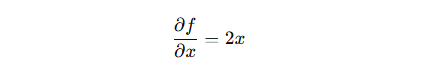
これは、平面上で xx 軸方向の傾きを表します。同様に、yy 軸方向の傾きは:
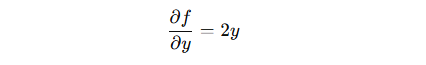
3. 最適化問題への応用
偏微分を用いて多変数関数の最大値や最小値を求めることができます。
例:
利益 P(x, y) を原料 x と労働量 y に依存する関数として、偏微分によって利益を最大化する x と y の値を求めます。
具体例
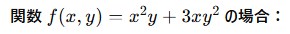
1.x による偏微分:
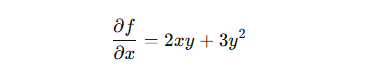
2.y による偏微分:
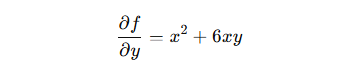
これにより、x と y のそれぞれの変化が 関数 f(x, y) に与える影響を調べることができます。